Quantum Mathematical Physics

Properties of most realistic models for gravity and/or gauge interactions at a cosmological level are highly dependent on their mathematical properties. Furthermore, modern approaches to the developments of detectors require of a profound knowledge of the properties of quantum systems and their interactions with classical ones. This research line focuses on this type of problems.

Thus, characterizing the entanglement in many-body systems, defining quantum field theories on arbitrary backgrounds, analyzing the impact that classically-controlled boundary conditions for quantum states may have in the dynamics of the quantum system or investigating the interaction of quantum fields and external time-dependent classical fields are some of the problems we consider:

Many body quantum systems

This line of research covers the study of emerging properties of Kitaev chains or other related many body quantum systems. We plan to discuss some of these properties as for instance:

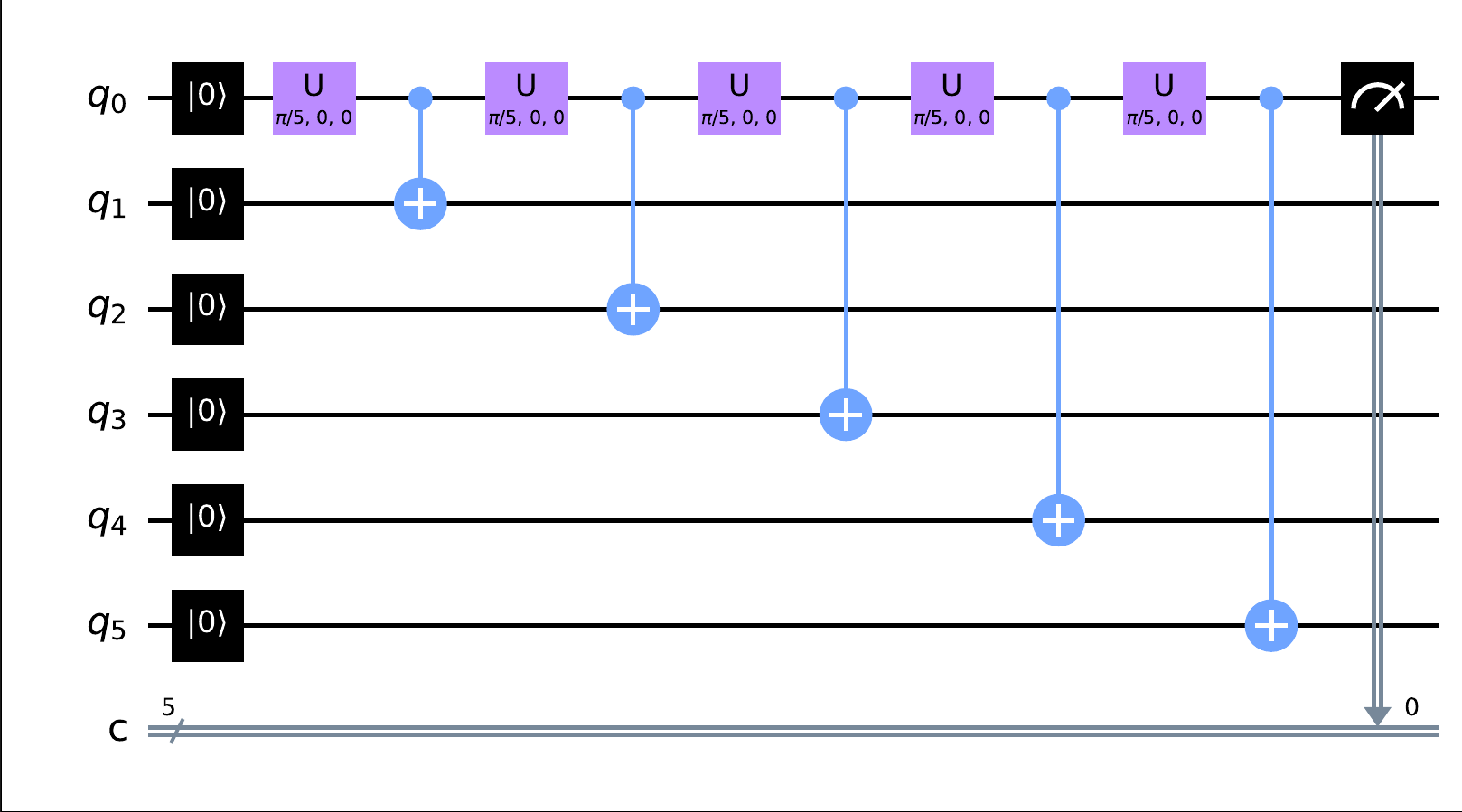
• Quantum Zeno effect (QZE) in a large quantum computer: we show that the multiple measurements that characterizes the QZE can be mimicked by the coupling of the system with many conditional gates. We consider that conditional gates couple the systems to multiple ancillas or that they all couple to a single one. We compare the dynamics of both situations and show similitudes and differences with the standard QZE [3]. We plan to continue this research implementing this ideas in real quantum computers and exploring the possible applications to stabilize qubits in quantum computers.
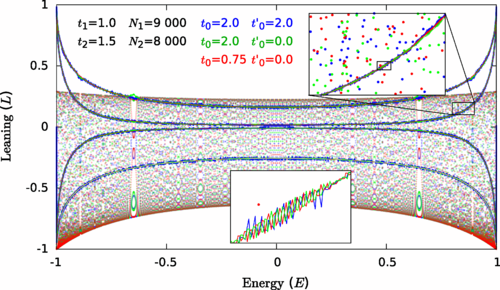
• Leaning in heterogeneous Kitaev chains: here we discuss the distribution of the probability of presence of a particle in the two sides of a heterogeneous Kitaev chain. We have shown a remarkable pattern that shares properties with chaotic systems[4]. We plan to pursue this study to obtain a more accurate description of the phenomenon in terms of probability distributions and its universal properties
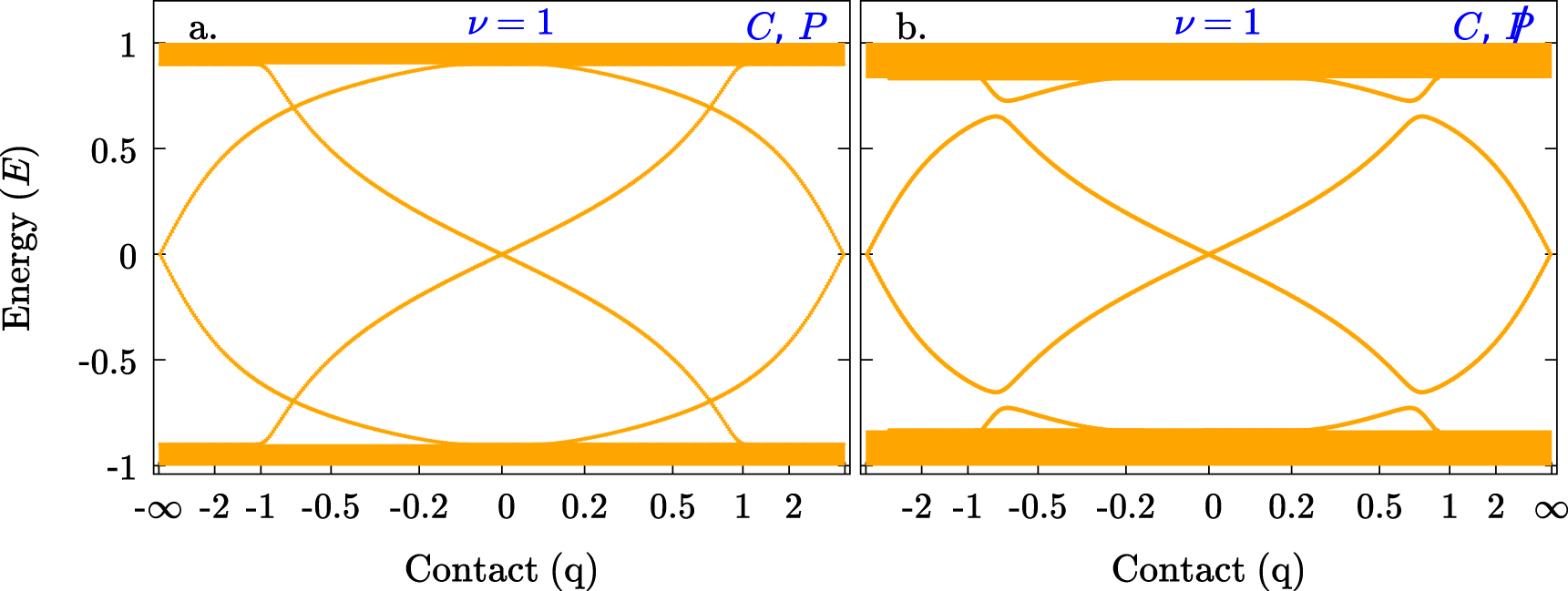
• Topological insulators in Kitaev chains with a defect: We study a fermionic chain with insulating behavior in the bulk. When it contains a defect, localized states may appear whose energy form a discrete spectrum between the valence and conduction bands. Modifying the couplings in the defect the states can migrate from a band to the other, imitating the properties of topological insulators that can transport charge or spin through states localize at the boundary[5]. The robustness of this mechanism is currently under study using topological invariants like the Berry curvature and others.

Boundary effects in quantum field theories

Different aspects of fluctuations of quantum fields in the vacuum are studied. When these fluctuations are modified due to the presence of some external conditions, they give rise to a net energy that could develop in a macroscopic measurable effect. The so-called vacuum energy or Casimir effect could play an important role at the micro and nanoscale but at the same time could also contribute to the dark energy. The second type of contributions leads to a too large effective cosmological constant which generates one of the fundamental problems of the compatibility of the Standard Model of particles and the current cosmological model LCDM.

We also ultimately expect that the analysis of the reaction of the vacuum to the presence of boundaries will shed some light on the non-perturbative behavior of confining theories like QCD.

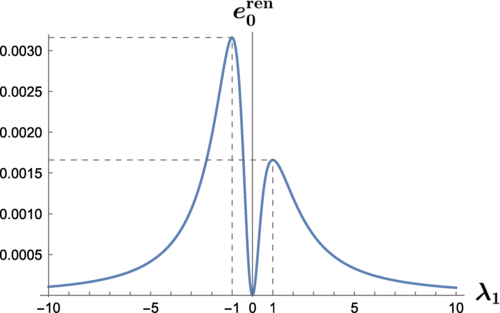
We focus on the study of the Casimir self-energy of compact objects as spheres or cylinders with different boundary conditions on their surfaces and considering both fluctuating scalar and vector fields. We study the divergences arising from this kind of calculations and identify the origin of some divergent terms. Unlike divergences found in quantum field theories, those coming from quantum vacuum energies cannot be treated with standard methods and new regularization methods have to be employed for each particular case. Interacting Casimir energy between bodies usually gives finite effects, meaning it is easier to extract the finite part, contrary to the study of self-energies, one more reason to assure that a full understanding of this effect requires that we take a close look at the divergences in order to understand its meaning.

Hybrid quantum-classical systems

Hybrid quantum-classical systems are dynamical systems where classical and quantum degrees of freedom evolve coupled to each other. Usually, they are approximations to full quantum models where some of the degrees of freedom correspond to particles with mass much higher than others and which therefore evolve with much longer characteristic times. These heavier and slower particles can be accurately described by classical models and therefore the whole system can be modeled by a combination of these classical objects interacting with the remaining quantum degrees of freedom used for the light and quick particles. The best known example for this type of dynamical system are molecular systems where nuclei and inner electrons can be described as a classical subsystem which interacts with the valence electrons. These valence electrons must keep a quantum description if we want to model accurately some physical phenomena as chemical reactivity or photo-induced processes such as photosynthesis. The interaction of a quantum system and a classical measuring device also fits within this framework, even if the problem becomes extremely complicated by the large difference in scale. In these approaches, the extension to statistical mechanical models based on hybrid dynamics is a natural requirement because of the macroscopic nature of the classical domains.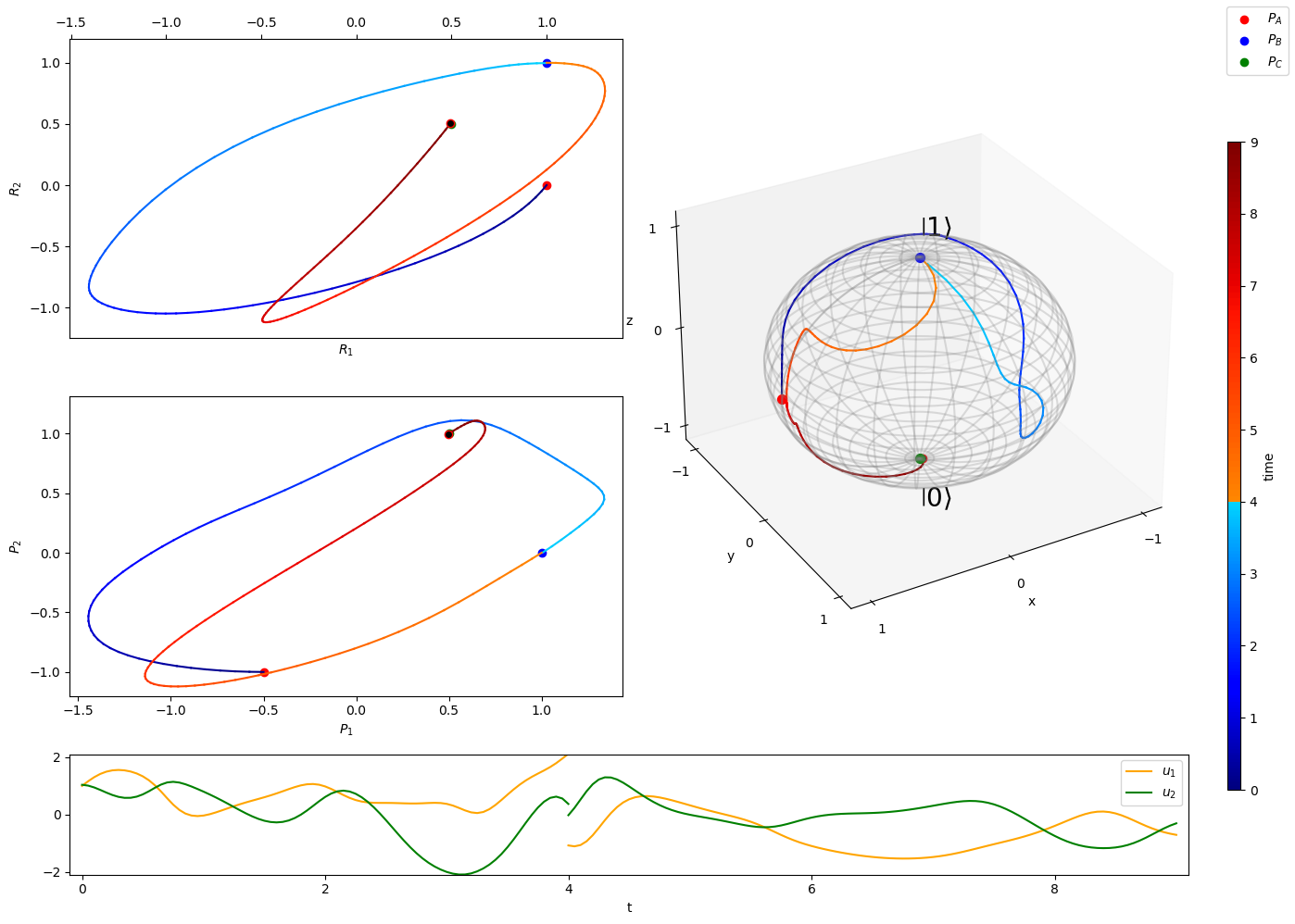

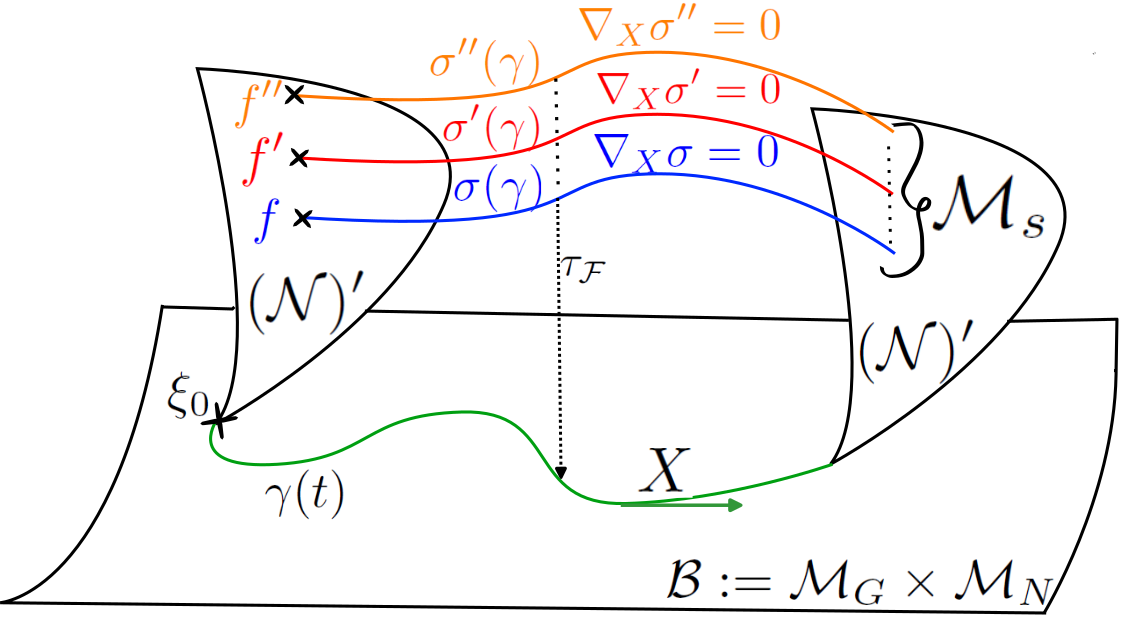
But we can find a similar situation when considering field theoretical models. Indeed, we can also consider a model where a quantum field theory interacts with a classical field. Several interesting examples fit in this framework, the most remarkable one being a quantum field theory which evolves in a given gravitational background. In this situation, models based on Minkowski-backgrounds field theories fail and all ingredients in our model must be reconsidered. Our approach is based on Malliavin stochastic calculus which provides rigorous mathematical tools to operate on spaces of fields modeled as Hida functions or distributions defined on the space of classical fields. These sets admit rigorously defined Gaussian measures and therefore square integrable functionals depending on classical degrees of freedom become meaningful. States become sections of suitable bundles defined on the space of classical objects and such dependence requires of the definition of a suitable connection to capture the effect on the quantum state of a change in the classical parameter. The simple case of scalar quantum field models is being considered now but more general cases will be analyzed in the future. Besides the case of external gravitational classical fields we plan to expand the framework to other cases of quantum-classical interactions such as the Casimir or the Schwinger effects.