Extending General Relativity

A fundamental component of the physical universe which is beyond the Standard Model is the gravitational interaction which in fact was the first discovered interaction. So far Einstein's theory of General Relativity describes quite successfully the gravitational interactions in a wide range of physical scales from the millimeter to intergalactic scales. However, there are few reasons to expect a modification of the theory at very short and very large scales. At large scales the apparent failure in the explanation of the rotating curves of galactic halos is actually solved by adding a dark matter component which also helps in fitting the current cosmological data.

Beyond General Relativity

The inflationary model which best fits the observational data is the Starobinsky model which involves a modification of Einstein theory by means of an $\mathbb{R}^2$ term (see Figure where the dependence of the ratio of the tensor-scalar fluctuations on the primordial tilt $n_s$ is analyzed according to Planck results).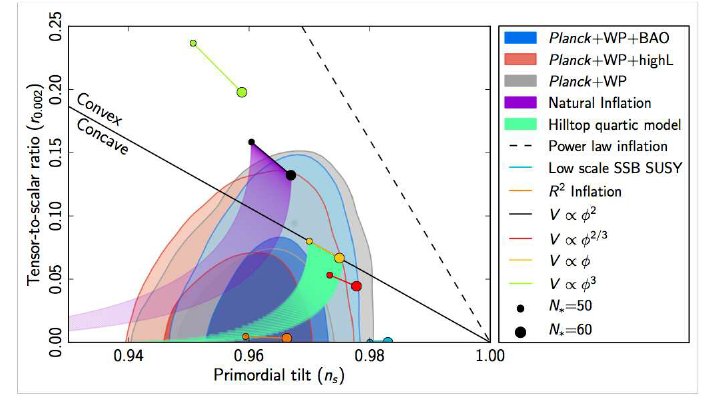 The increasing amount of data coming from cosmological observations and multi-messenger astrophysics of black hole (BH) mergers provide new sources of information that make possible tests of the relevance of these quantum effects in gravity.
Another argument that leads to consider Einstein's theory as an effective theory of a more fundamental one is its non-renormalizability as a quantum field theory.
This problem can be cured by introducing high derivative terms generalizing Starobinsky model or even non-local terms. All these theories are renormalizable but most of them present consistency problems related to violations of causality and unitarity. Another effect of these theories is that in spite of the fact that they do not have ultraviolet divergences they present Black Hole solutions with peculiar properties and a dynamics quite different from Einstein theory Black Holes.
The research line of CAPA to approach this problem has the following fundamental goals:

• Complete Einstein's theory with higher derivative terms to achieve a consistent theory of quantum gravity.
• Explore the behaviour of the different theories of gravity at scales below the millimeter scale to find possible deviations from General Relativity.
• Analyse the black hole physics of higher derivative theories of gravitation and its implications for binary black hole mergers.

Hybrid geometrodynamics

Another approach to this generalization of General Relativity is to consider an interaction with quantum matter fields. In this case, we generalize the Hamiltonian picture of General Relativity coupled to classical matter, known as geometrodynamics, to the case where such matter is described by a Quantum Field Theory in Curved Spacetime, but gravity is still described by a classical metric tensor field over a spatial hypersurface and its associated momentum. Thus, in our approach there is no non-dynamic background structure, apart from the manifold of events, and the gravitational and quantum degrees of freedom have their dynamics inextricably coupled. Given the Hamiltonian natureof the framework, we work with the generators of hypersurface deformations over the manifold of quantum states.

The construction relies heavily on the differential geometry of a fibration of the set of quantum states over the set of gravitational variables. An important feature of this work is the use of Gaussian measures over the space of matter fields and of Hida distributions to define a common superspace to all possible Hilbert spaces with different measures, to properly characterize the Schrödinger wave functional picture of QFT in curved spacetime. The most remarkable physical features of the construction are norm conservation of the quantum state (even if the total dynamics are non-unitary), the clear identification of the hybrid conserved quantities and the description of a dynamical backreaction of quantum matter on geometry and vice versa, which shall modify the physical properties the gravitational field would have in the absence of backreaction.